 |
Product Detail: |
 |
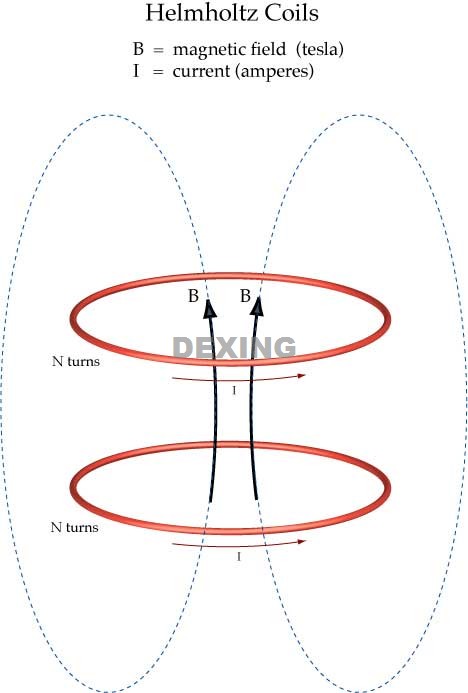
Helmholtz Coils
Helmholtz Coil
Introduction of Helmholtz Coil:
Hermann von Helmholtz (1821-1894)
German scientist and philosopher who made fundamental contributions to physiology, optics, electrodynamics, mathematics, and meterology.
Helmholtz Coils
A pair of conducting circular coils each having N turns, each carrying a current I, separated by a distance equivalent to the radius of the circular loops, produce a homogeneous magnetic field B in the mid-plane between the two circular coils.
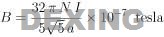
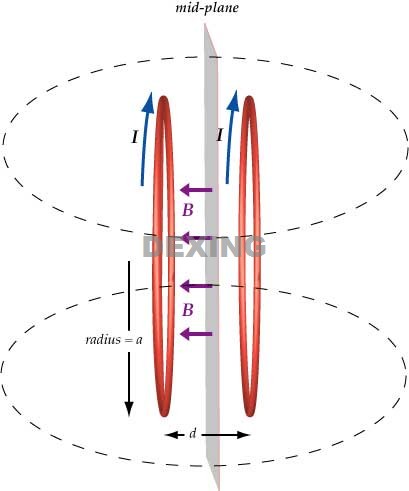
a = radius of the coils
a = separation between the coils
a/2 = distance to the mid-plane
B = magnetic field at the mid-plane |
 |
What creates a magnetic field?
A magnetic field is created whenever charge is in motion--either moving in space or spinning around itself. A charge moving in space is called a "current" (denoted by the symbol I) and is measured in coulombs/sec or amperes.
The strength of magnetic field is measured at a point in space (often called the field point). In the case of the Helmholtz coils, the field points of interest are located in the mid-plane between the two coils. As shown in the equation above, the strength of the magnetic field is dependent upon three quantities:
the current I,
the number of turns N in each coil, and
the radius a of the coil.
The total current in each coil is NI. |
 |
How uniform is the magnetic field?
The "claim to fame" for the Helmholtz coil is its very uniform magnetic field. However, the question that naturally arises , "how uniform, and over what distance?" To determine the uniformity of the magnetic field requires more than the above equation and involves some complicated integral calculus. However, we can generate some figures that graphically show how the magnetic field varies on the mid-plane as a function of r (the distance from the axis of symmetry passing between the centers of the two coils) and d the separation between the two coils. |
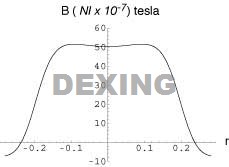 |
Coil spacing is "too close."
d = 0.8 a |
In the figures to the right, we can see how uniform the magnetic field is on the mid-plane when the spacing d is too close, just right, and too far. The figures to the right are calculated for coils with a radius of 20 cm (i.e., a = 0.20 m).
The following integral was evaluated to produce the three curves at the right. |
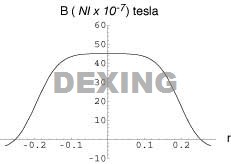 |
Coil spacing is "just right."
d = a |
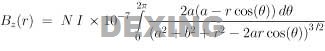
where the factor of "2" in the numerator takes into account the two coils, and b = d/2 is the distance from each coil to the mid-plane.
|
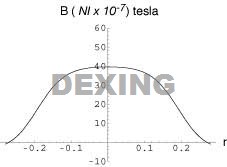 |
Coil spacing is "too far."
d = 1.2 a |
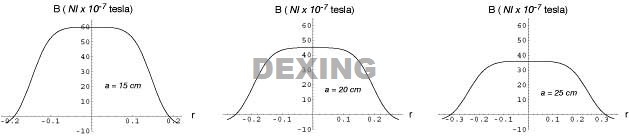
How does the region of uniform magnetic filed vary with the radius of the Helmholtz coils?
The figures below show the range of uniform magnetic field as a function of the coil radius.







.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
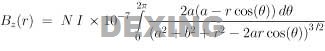
 Hysteresis Graph Test System
Hysteresis Graph Test System